Übung verkettete e-Funktion I
Weiter geht es mit den Übungen: Nach denen zur ln-Funktion gibt es nun auch eine zu der e-Funktion. Prinzipiell ist diese genauso aufgebaut wie die anderen Aufgaben auch: Zunächst die Angabe, dann die Lösungen auf verschiedene Art und Weise und danach ein paar Voraussetzungen, die beim Lösen bzw. beim Verstehen der Lösung weiterhelfen könnten.
Aufgabe
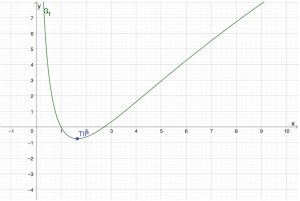
Gegeben ist die Funktion f mit f(x)=(x^2-4)e^x in ihrer maximalen Definitionsmenge D_f = \mathbb{R} und mit ihrem Graphen G_f.
1. Bestimmen Sie alle Schnittpunkte von G_f mit den Koordinatenachsen.
2. Untersuchen Sie das Verhalten der Funktionswerte f(x) für \vert x\vert \to\infty und geben Sie damit Art und Gleichung der Asymptote von G_f an.
3. Ermitteln Sie dei maximalen Monotonieintervalle von G_f und geben Sie damit Art und Lage der Extrempunkte von G_f an. Runden Sie gegebenenfalls auf zwei Nachkommastellen.
4. Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f.
Lösungen
Lösungen e-Funktion I
Prerequisites
- Was sind die grundlegenden Eigenschaften der e-Funktion?
- Wie leitet man ab (insbesondere mit der Produktregel)?
- Wie bestimmt man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie kann man Ungleichungen lösen (z.B. für VZ-Tabellen der Ableitung)?
Tierpark Bad Mergentheim
Hatte zuletzt ein spannendes Wochenende und kann auch alles durch Bilder belegen: Beim Klettern in den Alpen habe ich zufällig einen Steinbock gesehen. Danach habe ich etwas gebadet, aber leider hat mir ein Otter die Klamotten geklaut. Zum Glück Schafe gefunden, mir geschnappt, geschoren und erst Wolle und dann neue Klamotten daraus gemacht.
Bin weiter in die Pyrenäen, war aber so anstrengend, dass ich etwas geschlafen habe. Zum Glück gerade noch rechtzeitig wach geworden, bevor die Geier an mir geknabbert haben (ich schlief wirklich fest). Weiter ging es in die Karpaten wo ich mir mit Bären ein Snickers geteilt und ein Rudel Wölfe mit meinen veganen Bratwürstchen angelockt habe. War daher noch hungrig und wollte mit einem Lockruf zur Paarungszeit einen Luchs animieren, eine Maus mit mir zu teilen; eine Waldohreule war leider schneller und mein Magen knurrte nach wie vor. Danach haben mir nette Leute ein gutes Restaurant empfohlen; die waren irgendwie aus einem anderen Holz geschnitzt als ich.
Oder vielleicht war ich auch einfach nur im Tierpark Bad Mergentheim…
Übung verkettete ln-Funktion II
Bei der ersten Übung war die ln-Funktion mit einer quadratischen Funktion verkettet. Bei dieser Übung ist die ln-Funktion nun anders verknuddelt. Ansonsten ist der Aufbau der Lösungen fast identisch zu der der letzten Aufgabe: Nach den Angaben gibt es die Lösungen auf verschiedene Arten, am Ende ist ein Teil dessen aufgeführt, was man wissen sollte, um die Lösungen eventuell besser verstehen zu können.
Aufgabe
Gegeben ist die Funktion f mit f(x)=3(\ln(x))^2-\ln(x^3) in ihrer maximalen Definitionsmenge D_f= \mathbb{R}^+ und mit ihrem Graphen G_f .
- Zeigen Sie, dass sich die Funktionsgleichung auch in der Form f(x)=3\ln(x)\cdot (\ln(x)-1) darstellen lässt. Bestimmen Sie die Nullstellen von f.
- Untersuchen Sie das Verhalten der Funktionswerte f(x) für x\to 0 und geben Sie damit Art und Gleichung der Asymptote von G_f an. Geben Sie auch das Verhalten der Funktionswerte für x\to \infty an.
- Ermitteln Sie die maximalen Monotonieintervalle von G_f und geben Sie damit Art und x-Koordinate des Extrempunkts vonG_f an.
- Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f.
Lösungen
Lösungen II
2. Verhalten der Funktionswerte, Asymptote
Für x\to \infty folgt f(x)\to\inftyAnderer Grenzwert: Für x\to 0^+ folgt f(x)\to\infty, denn 3\ln(x)\to -\infty und \ln(x)-1) \to -\infty \Rightarrow G_f hat eine senkrechte Asymptote mit der Gleichung x=0.
3. Monotonieintervalle
Als Ableitung erhalten wir mit der Produktregel aus f(x)=3\ln(x)\cdot (\ln(x)-1) nun: f'(x)=3\cdot \frac{1}{x}(\ln(x)-1)+3\ln(x)\cdot \frac{1}{x}=\frac{1}{x}\cdot (3(\ln(x)-1)+3\ln(x))=\frac{6\ln(x)-3}{x}. Aus f'(x)=0 folgt 6\ln(x)-3=0\Leftrightarrow 6\ln(x)=3\Leftrightarrow\ln(x)=\frac{1}{2}\Rightarrow x_1=e^{\frac{1}{2}}=\sqrt{e}.Z.B. mit einer Vorzeichentabelle erhalten wir f'(x)<0 für x<\sqrt{e} sowie f'(x)>0 für x>\sqrt{e}.Dadurch ergibt sich: G_f ist smf in ]0;\sqrt{e}] und G_f ist sms in [\sqrt{e};\infty[. Damit ist bei \sqrt{e} offensichtlich ein Tiefpunkt.
Auch bei dieser Aufgabe gibt es die Lösungen als PDF zum Download.
Prerequisites
- Wie wendet man Logarithmusgesetze an?
- Wie berechnet man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie wendet man die Ableitungsregeln an, insbesondere Produktregel?
Übung verkettete ln-Funktion I
Bisher beinhalteten die meisten meiner Beiträge und Seiten grundlegenden Stoff. Dies diente hauptsächlich dem Verständnis, doch natürlich gehört auch das Üben zur Mathematik dazu. Daher hier nun eine erst Übung – zu einer verketteten ln-Funktion.
Aufgabe
Gegeben ist die Funktion f mit f(x)=\frac{3}{2}\cdot \ln(-(x^2+6x+5)) in ihrer maximalen Definitionsmenge D_f\subseteq \mathbb{R} und mit ihrem Graphen G_f
- Bestimmen Sie die maximale Definitionsmenge D_f .
- Untersuchen Sie das Verhalten der Funktionswerte f(x) für x\to -1 .
- Berechnen Sie die Nullstellen von f.
- Bestimmen Sie Art und Koordinaten des Extrempunkts von G_f
- Zeigen Sie, dass der Graph von f keinen Wendepunkt besitzt.
Lösungen
Im Folgenden kann man seine Lösungen auf verschiedene Arten kontrollieren: Teilaufgabe für Teilaufgabe mit wenig Text aber den wichtigsten Rechnungen, als ausführlicheres PDF zum Herunterladen oder auch als (hoffentlich nicht zu langes) Video.
Ein Teil der Werkzeuge, die man zum Lösen eventuell nützlich finden könnte, sind dann weiter unten unter Prerequisites verlinkt.
Lösungen I
2. Grenzwerte
Annäherung von links: Wegen -(x^2+6x+5) \to 0^+ für x\to -1^+ und den Eigenschaften der ln-Funktion folgt\frac{3}{2}\ln(-(x^2+6x+5)) \to -\infty für x\to -1^+
3. Nullstellen
Weil \ln(1)=0 ist, muss -(x^2+6x+5)=1 sein. Es folgt -x^2-6x-5=1\Leftrightarrow-x^2-6x-6=0.Mit MNF: x_1=-3+\sqrt{3} und x_2=-3-\sqrt{3}. Beide Werte gehören zur Definitionsmenge von f.
4. Extrempunkte
Es ergibt sich: f'(x)=\frac{3}{2}\cdot\frac{1}{-(x^2+6x+5)}\cdot (-2x-6)=\frac{3}{2}\cdot\frac{-2x-6}{-(x^2+6x+5)}. Ansatz: f'(x)=0\Rightarrow -2x-6=0 (Bruch ist 0, wenn der Zähler 0 ist). Hieraus ergibt sich: -2x=6\Leftrightarrow x=-3Z.B. mit VZ-Skizze: Bei -3 VZ-Wechsel von + nach -, also ist dort ein HOP. f(-3)=3\ln(2)\Rightarrow HOP(-3\vert 3\ln(2))
5. Untersuchung Wendepunkte
Mit 2. Ableitung:
f''(x)=\frac{3}{2}\cdot \frac{-2\cdot(-(x^2+6x+5))-(-2x-6)\cdot (-(2x+6))}{(-(x^2+6x+5))^2} =\frac{3}{2}\cdot\frac{2x^2+12x+10-(4x^2+12x+12x+36)}{(x^2+6x+5)^2}=\frac{3}{2}\cdot\frac{-2x^2-12x-26}{(x^2+6x+5)^2}Ansatz: f''(x)=0 \Rightarrow -2x^2-12x-26=0Diskriminante MNF: D=12^2-4\cdot (-2)\cdot (-26)=-64 \Rightarrow Keine NS der 2. Ableitung, kein Wendepunkt.
Hier sind die Aufgaben und Lösungen als PDF zum Download.
Prerequisites
- Wie kann man Ungleichungen lösen?
- Wie berechnet man Grenzwerte (bei gebrochenrationalen Funktionen)?
- Wie sind die grundlegenden Eigenschaften der ln-Funktion? (Nullstelle, Definitionsbereich,…)
- (und 5.) Wie wendet man die Ableitungsregeln an, insbesondere Ketten- und Quotientenregel?
Die ln-Funktion
Im Video werden die grundlegenden Eigenschaften der ln-Funktion mithilfe derer der e-Funktion hergeleitet. D.h. wer nicht so vertraut mit der e-Funktion ist, sollte vielleicht mit dieser Seite anfangen. Wer mit Logarithmen so gar nichts anzufangen weiß, der sollte sich vielleicht auch erst woanders umschauen…
Man kann sich ein Blatt mit einer Übersicht dieser Eigenschaften herunterladen, ganz am Ende (es ist nicht so weit bis dahin…) gibt es noch einmal Lernkarten zum Wiederholen der grundlegenden Eigenschaften.
Analoges Blatt
Hier das oben versprochene Übersichtsblatt
Digitale Übung