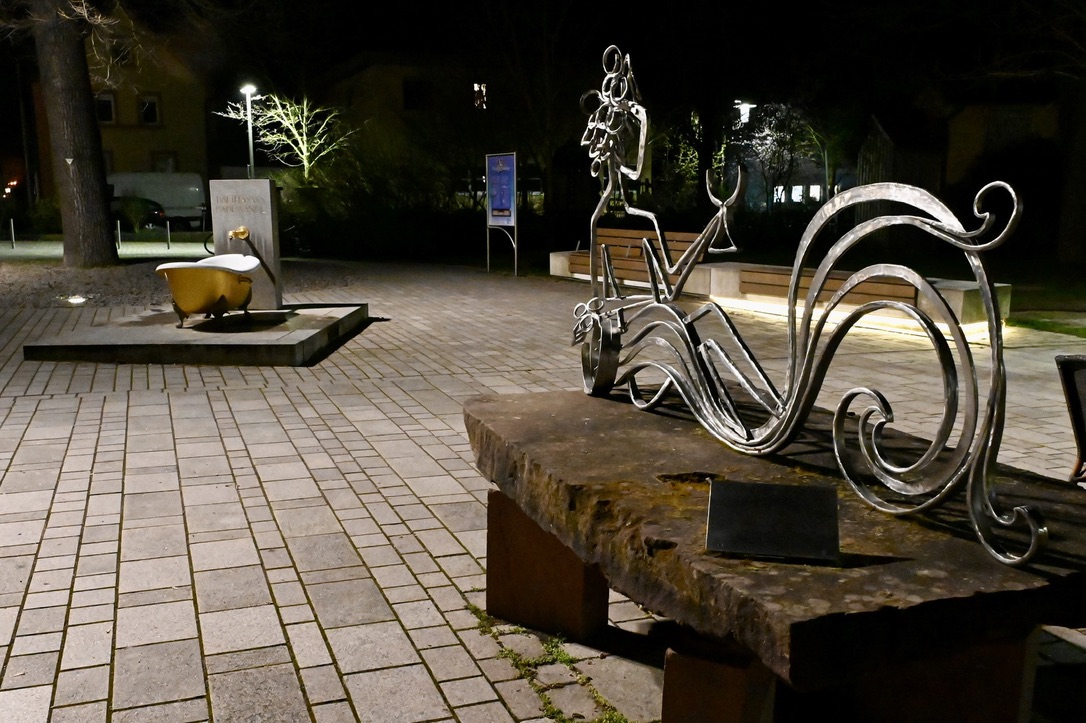Insekten
Wäre ich so riesenwinzig klein
und könnte sehen, was niemand sonst verstehen kann,
wäre ich nur Spielball großer Kräfte,
umhergewirbelt ohne Sinn mit Zwang.
Randersacker – Tag & Nacht
„Idyllisch hier!“, kann man sich denken, wenn man nach Mainfranken kommt. Etliche Ortschaften hier sind reizvoll anzusehen, sowohl was kleine Details als auch das Gesamtensemble angeht. Tagsüber und auch nachts.
Neben dem wunderschönen Eibelstadt, zu dem ich gerade auch einen Beitrag gemacht habe, gehört da ebenso Randersacker; ich denke, das zeigen die Bilder.
Eibelstadt – Tag & Nacht
„Idyllisch hier!“, kann man sich denken, wenn man nach Mainfranken kommt. Etliche Ortschaften hier sind reizvoll anzusehen, sowohl was kleine Details als auch das Gesamtensemble angeht. Tagsüber und auch nachts.
Natürlich gehören dazu auch die Weinberge, die sich oft außenrum befinden und die fast immer einen Spaziergang wert sind. Das zeigen die Bilder hoffentlich, die ich jetzt von Eibelstadt und in Zukunft auch von anderen Ortschaften aus der Gegend veröffentlichen werde.
Holz
Zur Natur gehört nicht nur das Lebende, sondern auch das Gegenteil, z.B. Totholz. Abgestorbenes Holz ist nicht nur ein wichtiger Bestandteil des Ökosystems Wald, es kann auch recht hübsch oder zumindest interessant anzusehen sein.
Ich hoffe, die folgenden Schwarz-Weiß-Bilder zeigen dies etwas.
Übung verkettete e-Funktion II
Aufgabe
Gegeben ist die Funktion f mit der Funktionsgleichung f(x)=\frac{e^x-4}{e^x+1} in ihrere maximalen Definitionsmenge D_f=\mathbb{R} und mit ihrem Graphen G_f.
1. Bestimmen Sie die Nullstellen von f.
2. Untersuchen Sie das Verhalten der Funktionswerte f(x) für x\to -\infty und geben Sie \lim_{x\to\infty} sowie Art und Gleichungen der Asymptoten von G_f an.
3. Ermitteln Sie die maximalen Monotonieintervalle von G_f.
4. Bestimmen Sie die Koordinaten des Wendepunkte von G_f.
5. Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f. Zeichnen Sie auch die beiden Asymptoten ein.
Lösungen
Lösungen e-Funktion II
Prerequisites
Was man können soll, ist nicht wesentlich anders, als bei der ersten Übung zur e-Funktion auch. Dennoch kann es ja nicht schaden, es hier aufzuführen:
- Was sind die grundlegenden Eigenschaften der e-Funktion?
- Wie leitet man ab (insbesondere mit der Quoientenregel)?
- Wie bestimmt man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie kann man Ungleichungen lösen (z.B. für VZ-Tabellen der Ableitung)?