Mathematik
Definition einer Umkehrfunktion
Um zu verstehen, was eine Umkehrfunktion ist, kann es nicht schaden, sich zunächst den Begriff eine Funktion genauer unter die Lupe zu nehmen. Dies passiert im ersten interaktiven Video. Neben der eigentlichen Definition geht es da auch darum, wie man sich den Funktionsbegriff veranschaulichen kann.
Mit diesem Rüstzeug können wir uns nun auch der Umkehrfunktion zuwenden. Im zweiten interaktiven Video werden die wesentlichen Eigenschaften von Umkehrfunkionen betrachtet.
Baumdiagramme erstellen
Baumdiagramme sind in der Stochastik wichtig, weil sie komplexe Zufallsexperimente übersichtlich darstellen. Schritt für Schritt lassen sich alle möglichen Ausgänge und ihre Wahrscheinlichkeiten visualisieren. Dadurch werden Abhängigkeiten oder Unabhängigkeiten klar erkennbar. Außerdem erleichtern Baumdiagramme (später auch) das Rechnen mit Pfadregeln und helfen, Fehler bei der Wahrscheinlichkeitsberechnung zu vermeiden.
Hier gibt es zunächst ein interaktives Video zum Erstellen davon, aus dem das Wesentliche klar werden sollte. Die dem Video zugrundeliegende PowerPoint-Präsentation kann man sich dann genauso herunterladen wie Aufgaben verschiedener Schwierigkeitsstufen dazu. Zu zwei der Aufgaben gibt es auch kurze Lösungsvideos.Analoge Materialien
- Die PowerPoint-Präsentation zum Video
- Einfache Aufgaben
- Mittelschwere Aufgaben
Lösungen
Die beiden Links sind direkt zu den entsprechenden Videos auf YouTube:
Aufgabe Wissenschaftler auf Kongress, Aufgabe WandererÜbung verkettete e-Funktion II
Aufgabe
Gegeben ist die Funktion f mit der Funktionsgleichung f(x)=\frac{e^x-4}{e^x+1} in ihrere maximalen Definitionsmenge D_f=\mathbb{R} und mit ihrem Graphen G_f.
1. Bestimmen Sie die Nullstellen von f.
2. Untersuchen Sie das Verhalten der Funktionswerte f(x) für x\to -\infty und geben Sie \lim_{x\to\infty} sowie Art und Gleichungen der Asymptoten von G_f an.
3. Ermitteln Sie die maximalen Monotonieintervalle von G_f.
4. Bestimmen Sie die Koordinaten des Wendepunkte von G_f.
5. Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f. Zeichnen Sie auch die beiden Asymptoten ein.
Lösungen
Lösungen e-Funktion II
Prerequisites
Was man können soll, ist nicht wesentlich anders, als bei der ersten Übung zur e-Funktion auch. Dennoch kann es ja nicht schaden, es hier aufzuführen:
- Was sind die grundlegenden Eigenschaften der e-Funktion?
- Wie leitet man ab (insbesondere mit der Quoientenregel)?
- Wie bestimmt man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie kann man Ungleichungen lösen (z.B. für VZ-Tabellen der Ableitung)?
Übung verkettete e-Funktion I
Weiter geht es mit den Übungen: Nach denen zur ln-Funktion gibt es nun auch eine zu der e-Funktion. Prinzipiell ist diese genauso aufgebaut wie die anderen Aufgaben auch: Zunächst die Angabe, dann die Lösungen auf verschiedene Art und Weise und danach ein paar Voraussetzungen, die beim Lösen bzw. beim Verstehen der Lösung weiterhelfen könnten.
Aufgabe
Gegeben ist die Funktion f mit f(x)=(x^2-4)e^x in ihrer maximalen Definitionsmenge D_f = \mathbb{R} und mit ihrem Graphen G_f.
1. Bestimmen Sie alle Schnittpunkte von G_f mit den Koordinatenachsen.
2. Untersuchen Sie das Verhalten der Funktionswerte f(x) für \vert x\vert \to\infty und geben Sie damit Art und Gleichung der Asymptote von G_f an.
3. Ermitteln Sie dei maximalen Monotonieintervalle von G_f und geben Sie damit Art und Lage der Extrempunkte von G_f an. Runden Sie gegebenenfalls auf zwei Nachkommastellen.
4. Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f.
Lösungen
Lösungen e-Funktion I
Prerequisites
- Was sind die grundlegenden Eigenschaften der e-Funktion?
- Wie leitet man ab (insbesondere mit der Produktregel)?
- Wie bestimmt man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie kann man Ungleichungen lösen (z.B. für VZ-Tabellen der Ableitung)?
Übung verkettete ln-Funktion II
Bei der ersten Übung war die ln-Funktion mit einer quadratischen Funktion verkettet. Bei dieser Übung ist die ln-Funktion nun anders verknuddelt. Ansonsten ist der Aufbau der Lösungen fast identisch zu der der letzten Aufgabe: Nach den Angaben gibt es die Lösungen auf verschiedene Arten, am Ende ist ein Teil dessen aufgeführt, was man wissen sollte, um die Lösungen eventuell besser verstehen zu können.
Aufgabe
Gegeben ist die Funktion f mit f(x)=3(\ln(x))^2-\ln(x^3) in ihrer maximalen Definitionsmenge D_f= \mathbb{R}^+ und mit ihrem Graphen G_f .
- Zeigen Sie, dass sich die Funktionsgleichung auch in der Form f(x)=3\ln(x)\cdot (\ln(x)-1) darstellen lässt. Bestimmen Sie die Nullstellen von f.
- Untersuchen Sie das Verhalten der Funktionswerte f(x) für x\to 0 und geben Sie damit Art und Gleichung der Asymptote von G_f an. Geben Sie auch das Verhalten der Funktionswerte für x\to \infty an.
- Ermitteln Sie die maximalen Monotonieintervalle von G_f und geben Sie damit Art und x-Koordinate des Extrempunkts vonG_f an.
- Skizzieren Sie mithilfe der bisherigen Ergebnisse möglichst genau den Verlauf von G_f.
Lösungen
Lösungen II
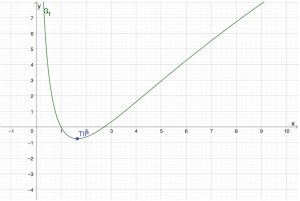
2. Verhalten der Funktionswerte, Asymptote
Für x\to \infty folgt f(x)\to\inftyAnderer Grenzwert: Für x\to 0^+ folgt f(x)\to\infty, denn 3\ln(x)\to -\infty und \ln(x)-1) \to -\infty \Rightarrow G_f hat eine senkrechte Asymptote mit der Gleichung x=0.
3. Monotonieintervalle
Als Ableitung erhalten wir mit der Produktregel aus f(x)=3\ln(x)\cdot (\ln(x)-1) nun: f'(x)=3\cdot \frac{1}{x}(\ln(x)-1)+3\ln(x)\cdot \frac{1}{x}=\frac{1}{x}\cdot (3(\ln(x)-1)+3\ln(x))=\frac{6\ln(x)-3}{x}. Aus f'(x)=0 folgt 6\ln(x)-3=0\Leftrightarrow 6\ln(x)=3\Leftrightarrow\ln(x)=\frac{1}{2}\Rightarrow x_1=e^{\frac{1}{2}}=\sqrt{e}.Z.B. mit einer Vorzeichentabelle erhalten wir f'(x)<0 für x<\sqrt{e} sowie f'(x)>0 für x>\sqrt{e}.Dadurch ergibt sich: G_f ist smf in ]0;\sqrt{e}] und G_f ist sms in [\sqrt{e};\infty[. Damit ist bei \sqrt{e} offensichtlich ein Tiefpunkt.
Auch bei dieser Aufgabe gibt es die Lösungen als PDF zum Download.
Prerequisites
- Wie wendet man Logarithmusgesetze an?
- Wie berechnet man Grenzwerte (z.B. bei gebrochenrationalen Funktionen)?
- Wie wendet man die Ableitungsregeln an, insbesondere Produktregel?